Transformer を理解したいので。
Transformer モデル構造
Transformer は大きく Encoder と Decoder の二種類に分けることができます。各ブロックは
- Attention
- Feed-forward network(FFN)
- Residual + Layer norm
から構成されており、Encoder と Decoder とも基本的な処理は同じなのですが使用する情報に差分があります。本記事では、
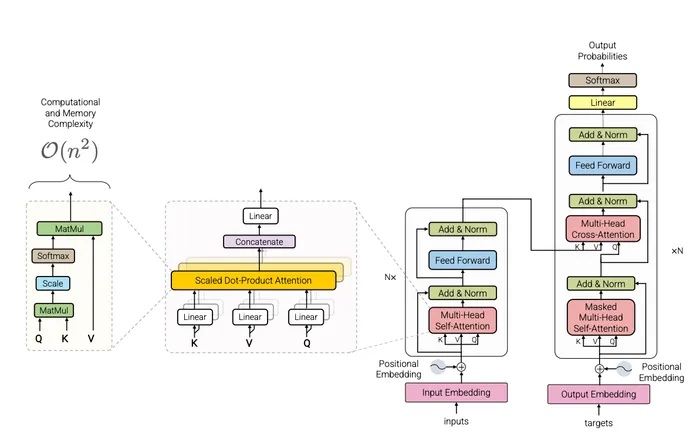
で表されている Transformer の構成についてを解説していきたいと思います。
Encoder / Decoder について
Transformer では、使用する情報や想定するタスクによって Encoder と Decoder の二種類の処理フローがあります。これらはモデル構造自体に大きな差分があるわけではなく、
- Encoder では、attention 部分に self attention を使用しており、双方向(未来)の情報を用いる
- Decoder では、attention 部分に masked self attention を使用しており、未来の情報を予測する
というように大別することができます。より漠然と捉えると
- トークン自体の埋め込み表現を計算したい場合は encoder
- トークン生成が目的なら decoder
として捉えても良いと思います。Transformer 元論文におけ左側か右側どちらを拝借しているかということです。
Encoder only
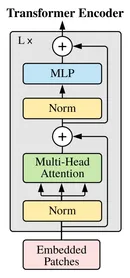
Encoder のみを使用しているモデルとして、BERT や ViT が挙げられます。self attention を使用していて、双方向(未来のトークンも見える)のスコアを計算します。BERT のように文章自体を分類することに特化している場合や、ViT のように画像全体の認識を行う場合には、情報全体を扱うために Encoder を使用するのが一般的です。
Encoder ブロックについて下図を引用しておきます。
Decoder only
Decoder のみを使用しているモデルとして、 GPT が挙げられます(Improving Language Understanding by Generative Pre-Training)。 デコーダーでは masked self attention を使用しており、未来のトークンとのスコアを計算しないようにマスクを掛けています。こうすることで、次トークン予測を行うモデルを作成することができます。
Decoder ブロックについて下図を引用しておきます。
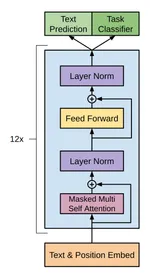
Encoder と比較してみると基本的には大差ないというのがわかると思います。
Encoder Decoder
Encoder と Decoder を使用しているモデルとして、元論文の Transformer や T5 が挙げられます。機械翻訳や文章要約など、入力情報の全体を把握しつつ、文章自体も生成するようなタスクで用いられています。
各種計算
ここからは、Transformer の計算が具体的にどうなっているかについてまとめていきたいと思います。
トークナイズ
Transformer は文字列をそのまま扱えないので、まず文字列からトークン列(整数のID列)へと変換します。OpenAIのモデルであればどのようにトークン化されるのかは https://platform.openai.com/tokenizer で確認することができます。 トークン化では、空白や記号も含めたトークンになることや日本語ではトークン数が増えやすい傾向にあることが見れると思います。


トークン分割・トークンIDはエンコーダーのモデル依存で、どういったモデルを使用するかによって変わってきます。
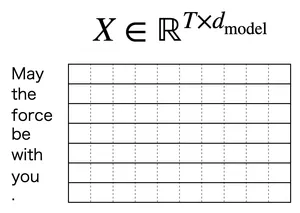
たとえば今回の場合だと、May the force be with you. は [13561, 290, 9578, 413, 483, 481, 13] というトークンIDに変換されます。このトークンIDは埋め込み行列からベクトルを取得するためのインデックスとなっていて、語彙サイズを、モデル次元数を とすると埋め込み行列は
となり、ここからトークンIDと対応する行番号のベクトルを取ってくることで入力情報を作成することができます。文章をトークナイズして得られたトークン列を埋め込み行列でベクトル化したものを、行方向に並べた行列を
- 系列長:
- モデル次元:
として
が得られます。以降は 1トークン = 1行ベクトル( は の 行目)という約束で進めます。行ベクトル / 列ベクトルの流儀は文献によって異なりますが、どちらでも数学的には同じ内容です。行ベクトルでの定義
は、列ベクトルでの定義に書き換えると
のように転置で対応づけられます。
Self-attention 機構
Transformer の中心的アイデアが attention であり、まずは self-attention について分解して理解していきたいと思います。 ここであえて self attention と明記したのは、cross attention と区別するためです。これらは
- self attention:Query / Key / Value を同じ系列 から作成
- cross attention:Query と Key / Value を作成する系列が別
という違いがあります。計算方法・考え方に大差はないので理論的には統一的に扱えますが、まずは self attention に絞ったほうが理解しやすいと思います。 以下では、
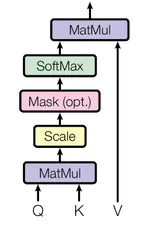
の計算の流れを追い、図と式が一対一で対応して理解できるようになることを目標とします。
(1)
Transformer は文字列そのものではなく、埋め込み済みのトークン行列 を入力として受け取ります。先程の例の
May the force be with you.
をトークン化して並べると、系列長 であるので
の形で表せます。
self attention では、各トークン を役割の異なる3種類の表現に線形変換して分けます。
ここで は学習される重み行列です。このとき各ベクトルの次元は
になります。
クエリベクトル の作成を例に取り、具体的な計算を以下に示します。
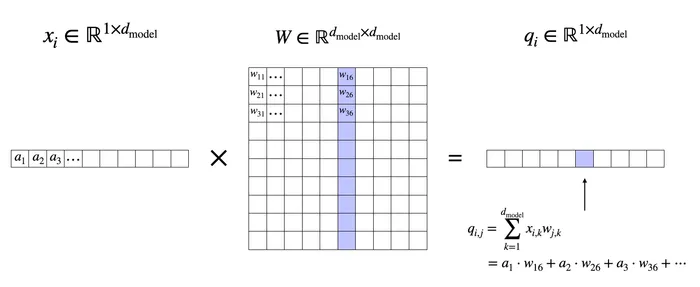
トークン のベクトル自体は定数であり、 の重みをかけ合わせた行列計算を行うことで
としてクエリベクトルの各成分が計算されます。
全体的な計算を俯瞰した後で「クエリ、キー、バリュー」という名前について考えるのが良いと思いますが、ひとまず直感的には以下の対応で理解しておくとよいです。
- Query(): 「いま自分(トークン )が注目したい特徴は何か」を表す検索条件
- Key(): 「各トークン がどんな特徴を持つか」を表すインデックス
- Value(): 「実際に集約して受け渡す情報の中身」
1トークンではなく系列全体に拡張すると、行列演算としてまとめて書けます。
それぞれ
で、行方向に が並びます。
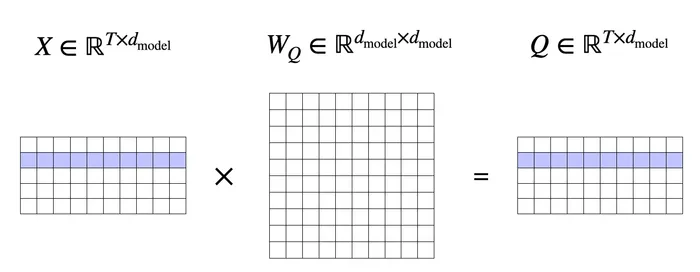
(2)
トークン同士の “関係性” を数値化するために、ベクトル同士の内積を計算します。クエリベクトル とキーベクトル との内積
を計算して、それらまとめます。 は行方向にクエリベクトルが並んでいること、 は転置しているので列方向にキーベクトルが並んでいることに注意すると、
の計算をすることで、全トークン同士の内積を計算した行列を作ることができます[1]。成分 は
です。例えば と との内積値 は以下のような形になります。
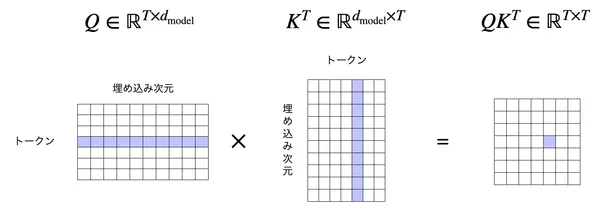
計算した は後段の処理で、トークン が をどれくらい参照したいかを表すスコアとして使用されます。
- 行(): 「どのトークンが」(参照する側 = Query 側)
- 列(): 「どのトークンを」(参照される側 = Key 側)
つまり は系列内の全トークン間の相関を一つの行列にしたものです。 この計算によりトークン同士をクロス集計した情報を表現することができます。
(3)
前節で得たスコア行列
は、各成分が内積
になっていて、「トークン (Query)がトークン (Key)をどれくらい参照したいか」を表す “生のスコア” です。ただしこのままだと値のスケールが大きくなりやすいので、正規化したうえで softmax を適用することで の確率値に変換します。
パラメーター で正規化し行方向にソフトマックス関数を適用した
が、attention matrix と呼ばれる情報です。計算した結果の に改めて着目すると下図のようになります。例えば3行目を見てみると、
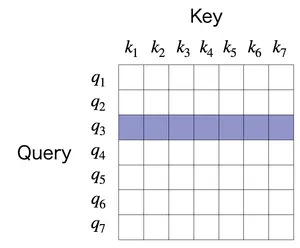
クエリ に対するキー との内積の値()にソフトマックス関数を適用した結果
が入っています。すると行方向は、クエリ に対しての全てのキー に対する “スコア” を計算する事ができ、クエリ がどのキーをどれだけの重みで参照したいかを表すことができます[2]。
また列方向では、列 はキー を固定して全てのクエリ がそれにつけたスコアが並んでいます。そのため、各クエリ からどれくらい重要と見なされているかの情報があります。 ただしソフトマックス関数は行方向に計算されているので、列方向の値を足しても1にはならず、単に大小だけが意味をなします。
(4)
前節 attention matrix までの計算で、
どこを重点的に見るかを表す情報を計算することができました。次にその重みを使って実際の特徴ベクトルを作成するかを計算します。attention matrix は softmax の演算が掛かっているので、トークンの情報は で内積値として混ざっているものの確率値になっているので特徴ベクトルとしてはそのまま使用できません。
そこで、バリュー を用いて
を計算します。
- (単純化して としてもよい)
なので
となり、各トークン位置ごとに新しい表現(混ぜた結果)が得られます。各行ごとにトークン由来のベクトルが入っているので、行ベクトルを として
のように の行列とみなせばより簡単に
と理解できるかと思います。
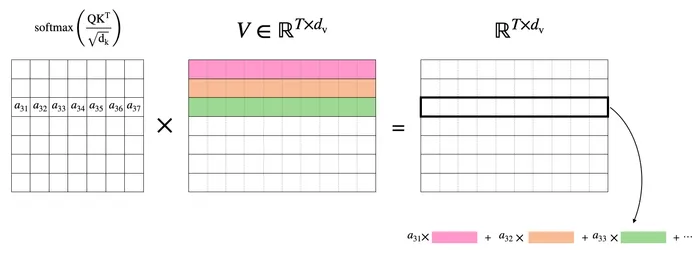
クエリがどのキーを参照するかの重みを計算できているので、その割合に従って value を混ぜる処理になります。ここでも例えば3行目に着目すると、それは の1行目を で重み付けしたものと、 の2行目を で重み付けしたものと、… との和になっている事がわかります。
そのため、例えば のような値(その他 のような場合)であれば計算したとの3行目はほとんど の3行目に等しいということになります。均等に が分布していればバリューを満遍なく取り込んだような値になります。このようにして、クエリ、キー、バリューを用いることで、系列同士の関係性を計算に落とし込むことができるのが attention 機構のロジックです。
ここまでの流れを全体で
ここまでの流れを全体的に示しておきたいと思います。トークン化された系列 は attention の計算を経て の行列が計算されます。元々の入力 と行列の形が同じであるので、それぞれはじめのトークン が他のどの情報を重要と感じているかを表す出力となっていることがわかります。
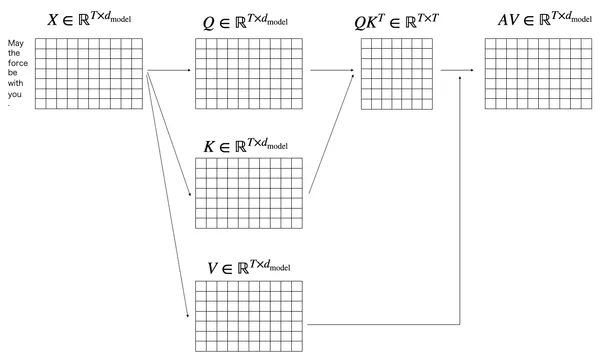
ここまで整理できれば

の に関する計算についてもできると思います。ただこの図の途中に Mask (opt.) という計算が挟まっていますが、ここについては一旦説明を後回しにして、作成した行列をどのように最終出力につなげるのかを先に説明します。
(5) Position-wise FFN
attention の計算でトークン間の情報のができたので、Transformer ブロックでは次に Position-wise FFN(Feed-forward networks) と呼ばれる計算を実行します。attention 処理では主にどのトークンに着目するかという発想で情報を収集してきましたが、次に作成した情報をどのように処理するかをこの Position-wise FFN で実行します。attention での出力を
とすると、Position-wise FFN は
の単なる feed-forward layers の処理です。ただし、行ごとに独立での処理で、各トークンの情報をそれぞれ何らかの特徴量として変換する処理であることに注意してください。
(6) スキップ接続
各 attention、Feed Forward 処理の前後を見ると skip connection があることがわかります。これはそのままの意味で、
となるようにそれぞれの処理の前後で入力情報を ResNet の要領で足していることを意味しています。
Masked self-attention
Transformer の self attention では、入力トークン行列 から
と作り、どのトークンがどのトークンをどれだけ参照するかを attention matrix として表現して
最終的な出力
を計算していました。成分で書けば、各位置 の出力は
であり、トークンを重み付きで混ぜ合わせる演算になっています。
なぜマスクが必要か
次トークン予測(自己回帰言語モデル)では、時刻(位置) の予測は の情報だけから行うことが前提です。例えば
- 入力:
May the force - 予測:次に来るトークン(例:
beなど)
という問題設定では、そのまま attention を計算すると
として be 由来の情報も混じってしまい()、モデルが訓練中に「正解トークン be(未来の情報)」を参照できてしまい、答えを見たうえで学習するために意味のある学習ができません[3]。
このリークを防ぐために、decoder-only Transformer では self attention を masked self-attention(causal self-attention) に置き換えます。
マスクの基本アイデア
masked self attention では、softmax の計算前にマスク行列 を加えます。
として落とします。ここで は「参照を許可しない場所を にする」行列です。典型的な因果マスク(causal mask)は
です。直感的には
- :過去・現在は参照してよい
- :未来は参照禁止(スコアを に落とす)
という意味になります。softmax の定義より、行 の重みは
です。もし なら なので
となり、結果として
になります。つまり未来トークンには重みが割り当てられないことが保証され、マスク部分はsoftmax 計算後にゼロとなり
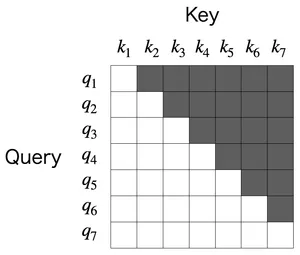
のように右上部分がマスクされた行列が出来上がります。これにより自分より未来の情報を含まず過去の情報だけを含む表現を作ることができます。
attention ブロック以降
Decoder-only Transformer ブロックは
- masked self-attention
- position-wise FFN
- residual / LayerNorm(順序は流派による)
です。このうち、トークン間の情報が直接的に混ざるのは self attention の部分だけで、 のバリューとの計算では係数でその混ざり具合が調整されています。
- FFN は position-wise:各位置 に同じ MLP を独立に適用するだけ
- LayerNorm は各トークンの特徴次元内の正規化であり、位置間を混ぜない
- Residual は同じ位置同士を足すだけで、位置間を混ぜない
したがって、自己回帰性(未来を見ない制約)を満たすためにはattention のスコアに因果マスクを入れるだけで十分です。
Cross-attention
ここまでの議論で、self attention は同じ系列 から を作り、系列内で情報を混ぜるものでした。
- 通常の self-attention:(マスクなし)
- masked self-attention: が因果マスク(未来参照禁止)
一方で cross-attention は、Query を作る系列とKey/Value を作る系列が 別である点だけが本質的な違いです。特に典型例は encoder-decoder Transformer(翻訳など)で、デコーダが「生成中のトークン(自分の状態)」を Query にし、エンコーダ出力(入力文の表現)を Key/Value として参照します。
cross attention の定義
Query 用の系列 と、Key/Value 用の系列 が別。
このとき attention は
で、式の形は self-attention と同じですが、 と の出所が違うことが決定的です。よくよく図を見直してみると、cross attention の部分だけ と とが別々のところからやってきているのがわかります。
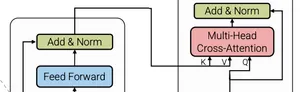
cross-attention では 2 系列の長さが一致する必要はなく、
- Query 系列長:
- Key/Value 系列長:
とすると、
から
となり、スコアと attention は
出力は
です。
成分での理解
成分で書けば、Query 側の位置 の出力は
です。ここで
- は Query 側(例:デコーダの生成位置)
- は Key/Value 側(例:エンコーダの入力文側)
になっています。
したがって cross-attention の直感は
- Query:いま生成している位置が「入力文のどこが必要か」を問い合わせる
- Key:入力文側の各位置が「自分はどんな情報を持つか」を示す索引
- Value:入力文側の実際の内容(混ぜて渡す中身)
です。
マスクについて
self-attention(自己回帰)では因果マスクが重要でしたが、cross-attention では基本的には未来の情報も使用します。翻訳タスクのように入力文はすでに与えられた系列であり、時系列的に禁止すべき“未来”が存在しないからです。一方でよく使うのは padding mask です。入力側系列 に PAD トークンが含まれる場合、その位置は参照しないように
- PAD 位置のスコアに を足す
というマスクを入れます。
タスクについて
Transformer ブロックの出力は、以下の図のように入力と同じ次元数です。
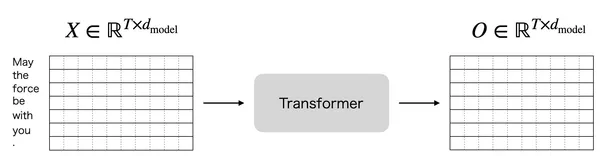
そのため、最終的なタスク(文章の感情分類や、次トークン予測)のためには何らかの方法で を処理して必要な次元数に加工する必要があります。
文章の分類など
BERT などで学習されている文章の分類タスクでは、一文が与えられた状態でそれについてのクラス分類を解きます。一文全体を入力として良いため、Transformer の encoder(self-attention ブロック)を使います。
BERT で用いられていた手法は、入力トークンに追加で [CLS] トークンと呼ばれる特殊トークンを追加するというものです。
[CLS] トークンを追加して Transformer ブロックに出力して、[CLS] トークンの位置に対応する行を取り出して最終的なクラス分類タスクを解くというものです。入力時点での [CLS] トークンのベクトルは全文章共通ですが、Transformer ブロックを通過するときにそれぞれの文章固有のベクトル表現になることが期待でき、それを用いた分類を行うという発想です。

次トークン生成など
GPT などで学習されている次に来る単語(トークン)の予測タスクでは、それまでのトークン列から次に来る確率の高いトークンを予測します。このときに May the force の次を予測するときに force 以降の情報を混ぜてはだめなので masked self-attention を使用する必要があり、そのため次トークン生成では Transformer decoder を使用します。
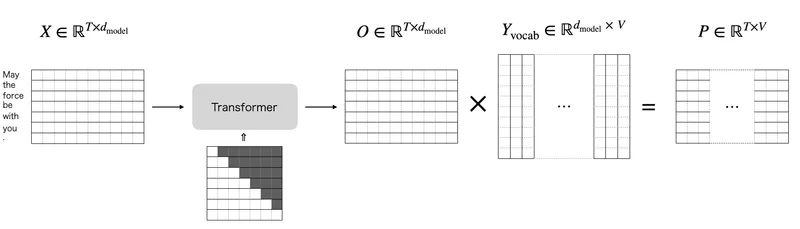
最終的には、 の出力になり、それぞれを次トークンに来ると予測するトークンとして解釈することができます。
脚注