クロスエントロピー(交差エントロピー)について、簡単に理論的背景を交えながら pyroch を用いた計算までをまとめました。クロスエントロピーを負の対数尤度関数として導出できる部分を知っていたほうが、より理解が深まると思っています。
それでは以下で実際にみていきます。
クロスエントロピー
多クラス分類問題に対してクロスエントロピー(交差エントロピー)は以下の式で定義されます。
$$ L = - \sum_{n=1}^N \sum_{k=1}^K p_{nk} \log \hat{p}_{nk} $$
ここでデータ $n$ に対してクラス $k$ である真の確率を $p_{nk}$、予測した確率を $\hat{p}_{nk}$ と表しています。
画像分類の例
簡単のためデータが1つの場合について考えてみます。
$$ L = - \sum_{k=1}^K p_{k} \log \hat{p}_{k} $$
とある画像識別モデルは画像を入力として、そのクラスを予測することができるとします。モデルは下図のように
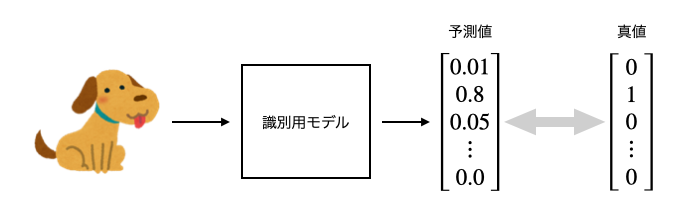
$K$ クラスのうち “どのクラスの画像っぽいか” の確率を要素として持つベクトルを予測値として出力します。真値として one-hot encoding したベクトルを用意しておくことで、これらの情報からクロスエントロピーを計算することができます。学習時にはこのクロスエントロピーを最小化するようにモデルパラメータを更新していくことになります。
対数尤度としての側面
天下り的にクロスエントロピーの定義式を導入しましたが、多クラス分類に関する尤度関数を計算することでも導出することができることを以下で見てみます。先程の例と同様に画像識別モデルを想定しますが、モデル部分をもう少しだけ詳細に(といってもパーセプトロンレベルの構造ですが)表現すると下図のようになります。
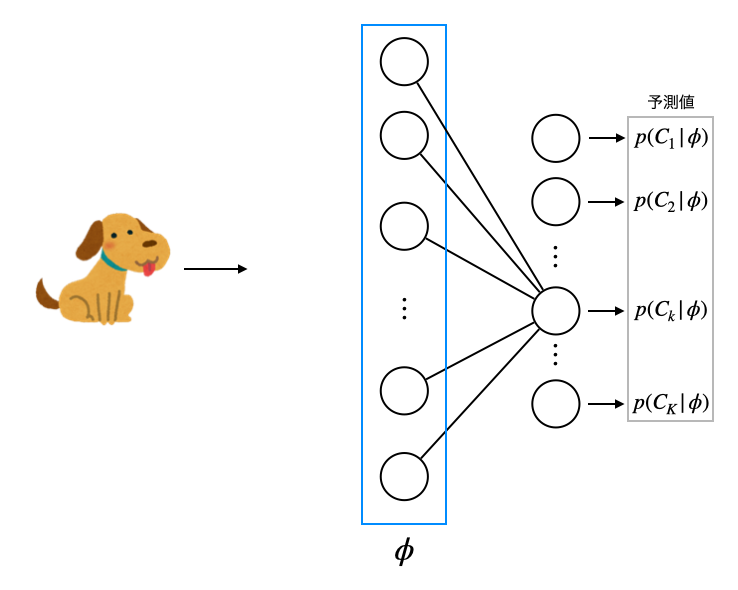
モデルの出力部分は入力情報を加工した情報(特徴ベクトル)を $\phi_n$ とすると、あるクラス $k$ に属する確率は
$$ p(C_k|\phi_n) $$
のように事後確率として表現することができます1。
ここでモデルのパラメータを最尤法を用いて決定するために、尤度関数を記述してみます。先ほどと同様にデータ $n$ 番目の画像がクラス $C_k$ に属する目的変数を $t_{nk}$ としておくと、尤度関数は
$$ L = \prod_{n=1}^N\prod_{k=1}^K p(C_k|\phi_n)^{t_{nk}} $$
として表現されます。最尤法では尤度関数を最大化しますが、ここで負の対数尤度を取りそれを最小化する方針としても同値です。負の対数をとると
$$ E = -\ln L = - \sum_{n=1}^N\sum_{k=1}^K t_{nk} \cdot \ln p(C_k|\phi_n) = - \sum_{n=1}^N\sum_{k=1}^K p_{nk} \cdot \ln \hat{p}_{nk} $$
となり、これは先程天下り的に導入したクロスエントロピーの式そのものです。
クロスエントロピー(交差エントロピー)は2つの確率分布の間で計算することのできる尺度で
$$ H(p, q) = - \sum_x p(x)\log q(x) $$
で定義されます。
PyTorch の実装
PyTorch で用意されている各損失関数についても確認しておきます。実際の数値計算の都合上、損失関数を定義しているクラスへの入力情報の加工についての取り扱いに注意しつつ議論していきます。
CrossEntropyLoss
入力
- input: softmax 処理を行っていないテンソル
- target: softmax 処理を行っているテンソル
注意点としては、nn.CrossEntropyLoss は softmax を掛けずにテンソルを渡す必要があります。そのためモデルの最終層で softmax を使用しているかどうかの確認が必須です。
使用例①
input に関しては内部で softmax 処理が適用される、target はそのまま使用されるということに留意して以下の使用例を見てみます。これはモデルがインデックス0番のクラスであると自身を持っている場合で、かつ真値もインデックス0番のクラスであるという場合ですが
>>> y_pred = torch.tensor([100, 1, 1, 1], dtype=torch.float32)
>>> y_true = torch.tensor([1, 0, 0, 0], dtype=torch.float32)
>>> loss = torch.nn.CrossEntropyLoss()
>>> loss(y_pred, y_true)
tensor(-0.)
クロスエントロピーとしては最小値を出しています。ただし少しややこしいことを見てみますが、モデルの出力が [1, 0, 0, 0] である場合には
>>> y_pred = torch.tensor([1, 0, 0, 0], dtype=torch.float32)
>>> y_true = torch.tensor([1, 0, 0, 0], dtype=torch.float32)
>>> loss = torch.nn.CrossEntropyLoss()
>>> loss(y_pred, y_true)
tensor(0.7437)
のようにクロスエントロピーとしては一定の値を持つことになります。これは y_pred は CrossEntropyLoss 内部で softmax 処理が実施されるため 2 実際には
>>> torch.log_softmax(y_pred, dim=0)
tensor([-0.7437, -1.7437, -1.7437, -1.7437])
の値を使って計算されるからです。CrossEntropyLoss を使用する際には以上のことに留意しながら検証を進めましょう。
使用例②
真値はクラスのインデックスを指定することもできます。このときには、2次元テンソルを使用する必要がありますが、以下のように入力することで同様の結果を得ることができます。
>>> y_pred = torch.tensor([[1, 1, 100, 1]], dtype=torch.float32)
>>> y_true = torch.tensor([2])
>>> loss = torch.nn.CrossEntropyLoss()
>>> loss(y_pred, y_true)
tensor(-0.)