論文情報
Abstract
- 高解像度タスク(super resolution; SR)に関する論文
- 蒸留(distillation)を使用することで、複数の scale factor に対応できる
- DDIM の 1-step での推論が SOTA 精度で可能になった
- 通常 200 step の部分が 1 step の denoising で置き換えられる
Introduction
拡散モデルでは denoising process の計算コストが大きく、Stable Diffusion のような latent space で計算しているようなモデルでも推論速度は遅いのが現状です。高解像度化(super resolution; SR)タスクに用いられる場合だと64×64のパッチを扱うことが多いのですが、ニーズとしては 256×256 の画像を 1024×1024 の画像へ4倍にアップサンプリングするようなものが多く、16個のパッチに対して処理を行う必要が生じます。そのため推論ステップ数の削減が一つの研究テーマとなってきています。
通常の画像生成との違いは、SR では低解像度画像(low-resolution; LR)の情報を条件付として高解像度画像(high-resolution; HR)を作成できることです。text-to-image タスクと異なり、作成したい画像に関する条件付が強いような比較的シンプルなタスクとしての側面を持っています(img-to-img の条件付に近いと思われます)。LR と HR の解像度の比率を scale factor と呼び、scale factor が小さいタスク(低解像度画像が程よい画質であるタスク)はより簡単なタスクとして位置づけられます。
YONOS-SR
Super resolution with latent diffusion models
super resolution タスクは、低解像度と高解像度 $(x_l, x_h)$ のペアを元にそれらが従う確率分布を予測することです。Stable Diffusion のフレームワークでは直接画像の情報を使っているのではなく、latent vector の情報を使っています。pre-trained encoder を $\epsilon$ としたときに $z = \epsilon(x)$ を使うということになります。super resolution タスクでは
- $z_t$:時刻 $t$ での予測値(latent vector での高解像度画像)
- $z_l$;入力の低解像度画像
の両方の情報を使用します1。つまり $p(z_h|z_t, z_l)$ を予測します。目的関数は
$$ {\rm{argmin}} E_{\epsilon, t} [\omega_t(\lambda_t) || \hat{z}_\theta (z_t, z_l, \lambda_t) - z_h ||_2^2 $$
で表されます。
Scale distillation
SR タスクの複雑さは “解像度” の違いに起因します。高解像度と低解像度とのスケールの違いをここでは scale factor(SF)と呼んでいますが、例えば SF を $\times 2$ にするために学習したモデルが、より低解像度な画像を入力とするときには推論ステップ数が増えてしまうということになります。それと比較して $\times 4$ で学習したモデルであれば end-to-end で推論ができてしまいます。
通常の学習では SF が固定されていたようですが、本論文では「Scale distillation」と呼ばれている学習手法を用いることでより柔軟な入力に対応できるということです。蒸留手法と同様に教師モデルと生徒モデルを擁し知恵、順次小さい SF の生徒モデルを学習していきます。
教師モデル、生徒モデルのパラメータをそれぞれ $\phi, \theta$ とすると、scale distillation loss は
$$ \underset{\theta} {\operatorname{argmin}} E_{\epsilon, t} \left[\omega_t(\lambda_t) || \hat{z}_\theta (z_t, z_l, \lambda_t) - z_\phi \left(z_t, z_l^\prime, \lambda_t \right) ||_2^2 \right] $$
で表されます。教師モデルは $2/N$ の SF で学習したモデルで、生徒モデルは $1/N$(教師モデルの半分)を学習します。以上のパイプラインが Fig.2 で示されています。
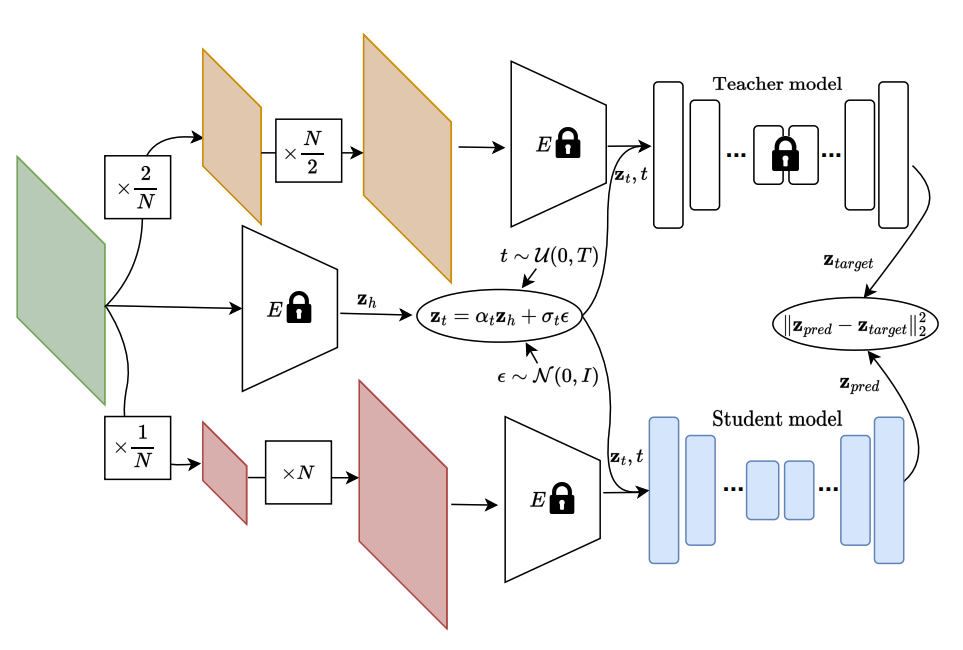
- 入力を $512\times 512$ (緑色)とする
- それぞれ $256\times 256$(黄色)、$128 \times 128$ (赤色)にする
- $512\times 512$ にアップサンプリングして入力とする
- pre-trained encoder に渡して、$4\times 64\times 64$ にする
結果
Stable Diffusion とYONOS-SR とを比較してみると、少ないステップでより高精度に高解像度化できていることが分かります。
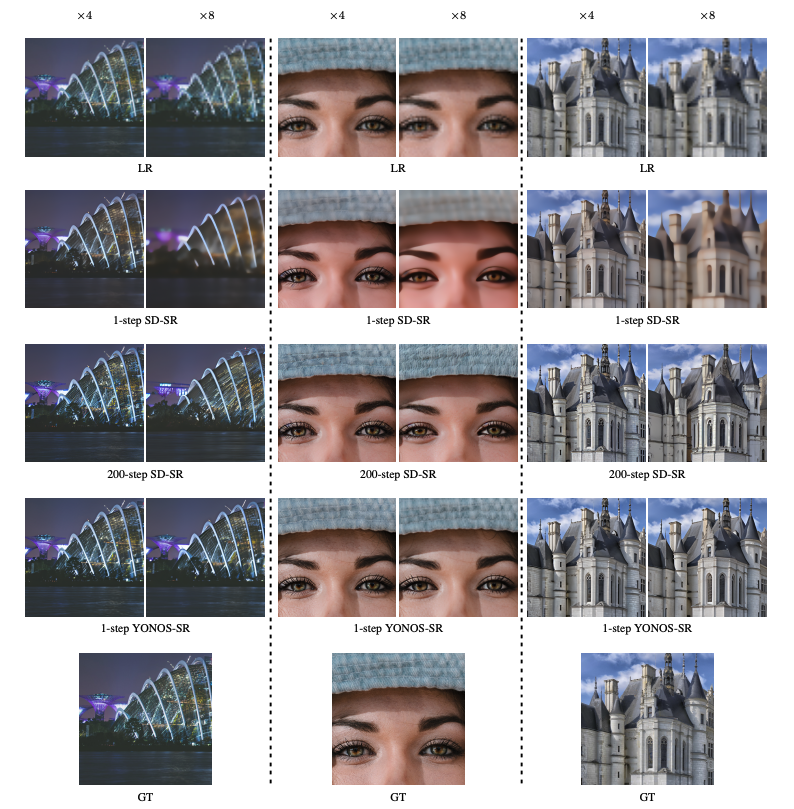
通常の Stable Diffusion では時刻 $t$ の予測値のみを使って $t-1$ の予測を行います。 ↩︎